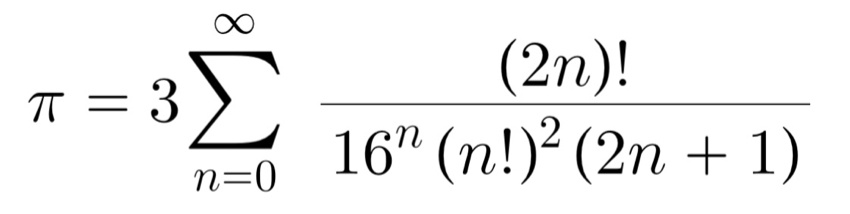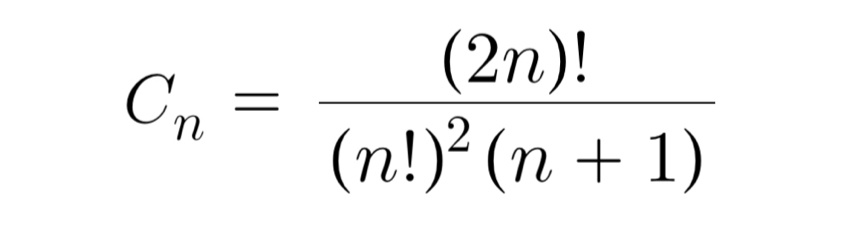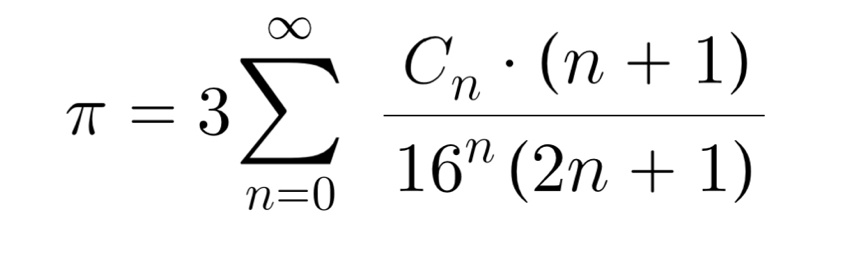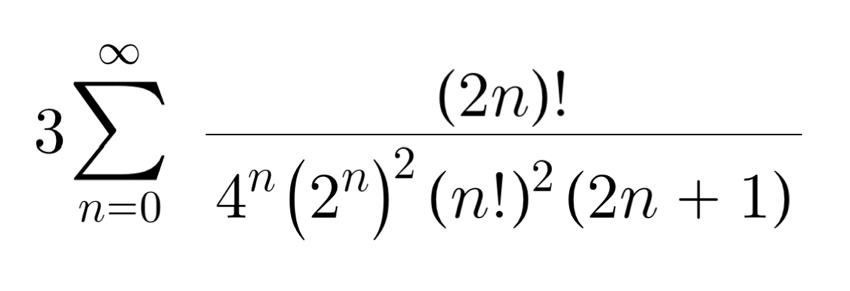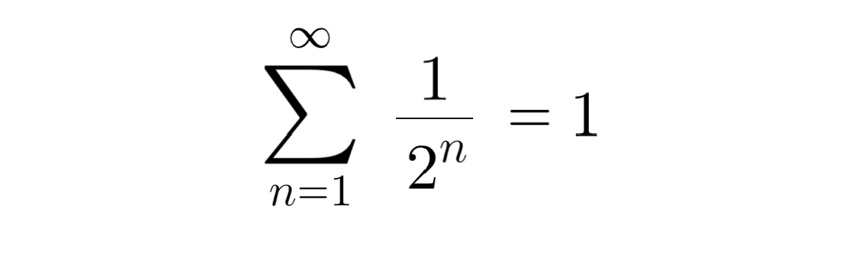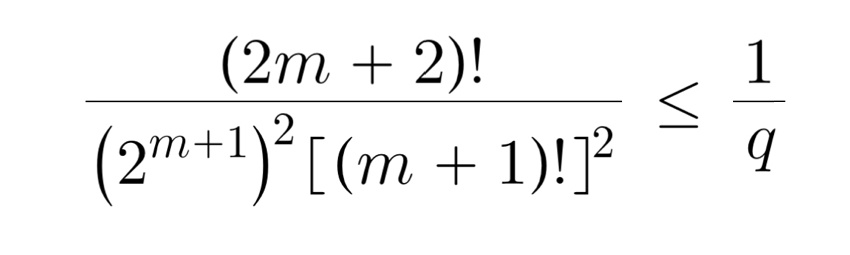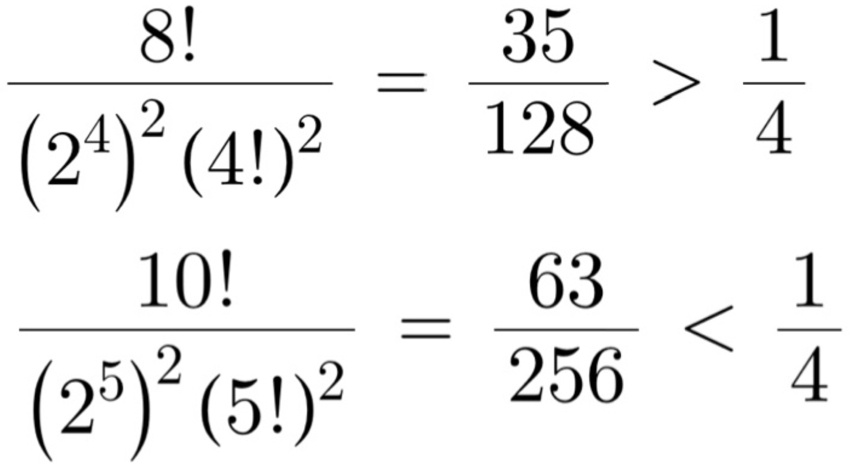ニュートンが作った、円周率の無平方根公式。
ニュートンの無平方根公式は、
以下の通り。
この式で、円周率の近似計算を
誤差評価も含めて下記の通り実施できる。
(2021-02-28、カタラン数について追記)
カタラン数 Cn は以下の通り表されるので、
より簡潔に公式を表現できる。
なお、カタラン数 Cn は整数になる。
(以上、2021-02-28の追記)
右辺を変形すると、
ここで、任意の負でない整数mを考え、
上式の∞をmにしたものをf(m) とすると、
であることから、
次式が成立することがわかる。
この右辺をg(m) とする。
ただし、qは次式をみたす任意の整数。
ここで、
(3×5) / (2×4×6) = 5/16 < 5/15 = 1/3
であることから、mが0か1であればq≦2,
mが2以上であればq≦3であることがわかる。
さらに、
であることから、mが4以上であれば
q≦4であることがわかる。
以上のことから、次表の通り
近似計算できる。
円周率が約3.14であることを計算するのは、
手計算でもじゅうぶんに可能。
表:円周率の近似計算結果
| m=0 q=2 | f(0)=3 g(0)=3.25 3 < π < 3.25 |
|---|---|
| m=1 q=2 | f(1)=3.125 g(1)=3.1625 3.125 < π < 3.17 |
| m=2 q=3 | f(2)=3.139.... g(2)=3.143.... 3.139 < π < 3.144 3.135 < π < 3.145 |
| m=3 q=3 | f(3)=3.1411.... g(3)=3.1420.... 3.141 < π < 3.143 3.14 < π < 3.145 |
| m=4 q=4 | f(4)=3.14151.... g(4)=3.14164.... 3.1415 < π < 3.142 |
| m=5 q=4 | f(5)=3.141576.... g(5)=3.141604.... 3.14157 < π < 3.14161 3.14155 < π < 3.14165 |
参考資料
資料は三つ。その内の、
次のふたつを資料にし、本ページでは
よりわかりやすく変形した式を掲載。
(変形前と同値であることを検証済。)
松元 隆二:円周率の公式集, Ver.3.141, 2000,
http://www.pluto.ai.kyutech.ac.jp/~matumoto/dvi/pi.pdf
中川 仁:円周率について, 上越教育大学, 2000,
https://www.juen.ac.jp/math/nakagawa/pi.pdf
また、中川氏の上記資料に加えて、
次の資料を参考にして、本ページでは
本題の式を「ニュートンの無平方根公式」
と称した。
後 保範:πを求める公式, 2002,
http://www.cs.t-kougei.ac.jp/nsim/method/piform.htm
本ページへのお問い合わせはこちら
ペンネームも
ニュートンの無平方根公式
です。
ページ公開日:2021-02-11
最終更新日:2022-02-11
Crayonホームページランキング
(個人・その他 - 週間)
(2021年2月13〜19日:1位! Thank you!)
[2021年2月14〜20日:1位! Thank you!]
:
: [7連覇! Thank you!]
:
[2021年2月19〜25日:1位! Thank you!]
(2021年2月20〜26日:8位! Thank you!)
(2021-02-27〜03-05:1位! Thank you!)
[2021-02-28〜03-06:1位! Thank you!]
:
: [7連覇! Thank you!]
:
[2021-03-05〜03-11:1位! Thank you!]
(2021-03-06〜03-12:7位! Thank you!)
https://crayon.e-shops.jp/ranking/week/iroiro/
(総合 - 週間)
(2021年3月18〜24日:2位! Thank you!)
(2021年3月19〜25日:2位! Thank you!)
https://crayon.e-shops.jp/ranking/week/
(個人・その他 - 月間)
(2021-02-11〜03-10:1位! Thank you!)
(2021-02-11〜03-11:1位! Thank you!)
(2021-02-11〜03-12:1位! Thank you!)
(2021-02-12〜03-13:1位! Thank you!)
(2021-02-13〜03-14:1位! Thank you!)
[2021-02-14〜03-15:1位! Thank you!]
:
: [連覇! Thank you!]
:
[2021-02-19〜03-20:1位! Thank you!]
[2021-02-20〜03-21:3位! Thank you!]
[2021-02-21〜03-22:1位! Thank you!]
:
: [13連覇! Thank you!]
: (12回連続防衛)
:
[2021-03-05〜04-03:1位! Thank you!]
[2021-03-06〜04-04:2位! Thank you!]
https://crayon.e-shops.jp/ranking/month/iroiro/
(個人・その他 - 年間)(見にいく166clicks!)
R03.02.11〜R04.02.10:29位! Thank you!
https://crayon.e-shops.jp/ranking/year/iroiro